Methods: A little bit about instrumental variables

Though there are lots of sources to learn about instrumental variables (IV), in this post I’ll point to three papers I found particularly helpful.

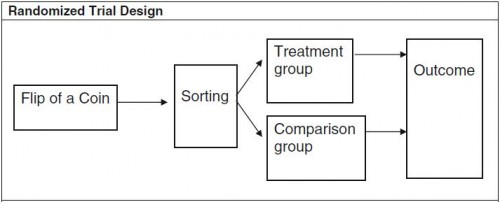
I’ve already written a tutorial post on IV, based on a paper by my colleague Steve Pizer. Two diagrams from that paper make clear that IV is a generalization of randomized controlled trials (RCTs). Conceptually, an RCT looks like this:

Randomization (e.g., by the flip of a coin) ensures that the characteristics of patients in the treatment and comparison groups have equal expected values. The two groups are drawn from the same sample of recruits and the only factor that determines their group assignment is the coin flip, so, apart from the treatment itself, all other differences between the groups must by construction be random.

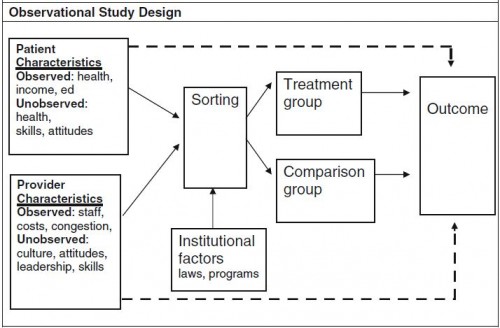
An IV study could look like the diagram below. Notice that if you ignore the patient and provider characteristics boxes on the left and the lines that emanate from them and interpret the institutional factors box at the bottom as a coin flip, this looks exactly like an RCT.

[In an IV study, a] large number of observed and unobserved factors [could] influence sorting into treatment and comparison groups. Many of these factors are also independently associated with differences in the outcome. These relationships are illustrated by the solid arrows connecting observed and unobserved patient and provider characteristics to sorting and the dashed arrows connecting these same characteristics directly to the outcome. The arrows directly to the outcome are dashed because these relationships are not the ones of primary interest to the investigator; in fact, these are potentially confounding relationships that could make it difficult or impossible to accurately measure the effect of treatment.

What makes an IV study an IV study is the analytical exploitation of some “institutional factors” (e.g., laws, programs) or other measurable features of the world—called instrumental variables—that affect sorting into treatment and control groups, at least somewhat, and are, arguably,* not correlated with any unobservable patient or provider factors that also affect outcomes. That’s kind of a mind-bender, but notice that an RCT’s coin flip has these properties: it’s a measurable feature of the world, affects sorting, and is not correlated with any unobservable patient or provider factors. Other things in the world can, arguably,* act like a coin flip, at least for some patients: program eligibility that varies geographically (like that for Medicaid), for example.

The algebraic expression of the forgoing difference between RCTs and IV studies by Katherine Harris and Dahlia Remler may also be informative to you (if you’re not math-averse). They consider patient i‘s health outcome, y_i, given by

[1]     y_i = β(h_i)d_i + g(h_i) + ε_i

where h_i denotes unobservable health status; d_i is a dichotomous variable that takes the value one if the patient is treated and zero otherwise; β(h_i) + g(h_i) is the expected health outcome if the patient receives the treatment; g(h_i) is the expected health outcome if the patient does not receive the treatment; and ε_i represents the effect of other unobserved factors unrelated to health status. The effect of treatment for each individual is the difference between health outcomes in the treated and untreated state, β(h_i). If treatment effects are homogenous, then β(h_i) = β for everyone. If treatment effects are heterogeneous, then β(h_i) is different for [at least some patients].

Next, the probability that patient i receives treatment can be written

[2]     P(d_i=1) = f(h_i) + z_i

where f(h_i) represents health status characteristics that determine treatment assignment, and z_i represents factors uncorrelated with health status that have a nontrivial impact on the probability of receiving treatment.

A potential problem in this setup is that treatment and outcome depend on health status h_i, which is unobservable. If unobservably sicker people are treated and are also more likely to have a bad outcome (because they are sicker), that will bias our judgment of the effect of treatment. The way out is to find or manufacture a z_i that determines treatment assignment for at least some patients in a way that is uncorrelated with unobservable health h_i (as well as uncorrelated with other unobservable factors that affect treatment, ε_i.)

In experimental settings, researchers strive to eliminate the effect of health status on the treatment assignment process shown in Equation 2 by randomly generating (perhaps in the form of a coin-flip) values of z_i such that they are uncorrelated with health status and then assigning subjects to treatment and control groups on the basis of its value. […]

In some nonexperimental settings, it may be possible to identify one or more naturally occurring  z_i, [IVs] that influence treatment status and are otherwise uncorrelated with health status. When this is the case, it is possible to estimate a parameter that represents the average effect of treatment among the subgroup of patients in the sample for whom the IV determines treatment assignment.

Harris and Remler go on to discuss more fully (with diagrams!) the subgroup of patients to which an IV estimate (aka, the local average treatment effect or LATE) applies when treatment effects are heterogeneous. With Monte Carlo simulations, they show that LATE estimates can differ considerably from the average treatment effect (ATE) one would obtain if one could estimate it for the entire population. Their explanation is beautiful and well worth reading, but too long for this post.

I’ll conclude with a shout out to one more worthwhile IV tutorial paper: the MDRC Working Paper “Using Instrumental Variables Analysis to Learn More from Social Policy Experiments,” by Lisa Gennetian, Johannes Bos, and Pamela Morris. As with the Pizer and Harris/Remler papers, it’s worth reading in full.

* “Arguably” because one needs to provide an argument for the validity of an instrumental variable. This is a mix of art and science, well beyond the scope of this post. I will come back to this in the future.