If you missed my last two posts on cost shifting theory, you might want to read them (part 1, part 2). This post does stand on its own, however. In it I’ll discuss a theory of hospitals under which cost shifting can occur, though theory alone can’t tell us the cost shift rate. Keep in mind that theory does not reflect all the richness of reality. It’s meant to give us some intuition about the world while avoiding the insurmountable challenges in precisely representing it.
All figures and quotes below are from David Cutler’s 1998 paper Cost shifting or cost cutting: the incidence of reductions in Medicare payments. As far as I know, it’s the only paper on cost shifting that provides a graphical theoretical treatment under utility (not profit) maximization.
Imagine a hospital that uses whatever profits it chooses to generate to subsidize unprofitable activities, such as care for the uninsured, teaching, research, or other investments. The hospital’s goal is not to maximize profits, but to maximize something else, generically termed “utility.” A function that characterizes utility can include profit, of course, but it must also include other activities–unprofitable stuff–too.
Consider the following figure for which price (on the horizontal axis) is the price paid by private (non-government) payers, assumed to be constant for all such entities for simplicity. Services (on the vertical axis) is also a one-dimensional abstraction of the variety of types and quantities of services hospitals provide.
Focus first on the profit function, ignoring for now the indifference curve. At one extreme, on the left half of the profit curve, the hospital is not providing some services that could earn it greater profit. As services offered increase, so does profit, up to a point. On the right half of the curve, the hospital is providing services that cost it more than the revenue it receives for them, decreasing profit.
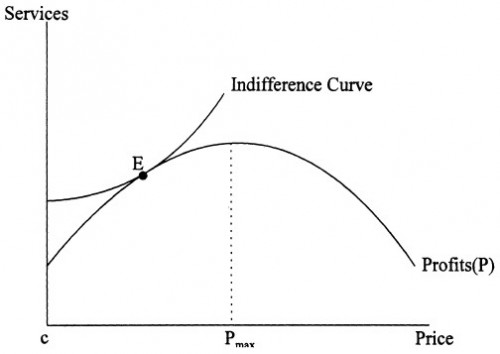
It is generally agreed that profit-maximizing firms will set price equal to Pmax, with the profits going to the hospital’s owners. But most hospitals are not for profit. Thus, the objective function of the hospital is not as certain. I assume that the hospital values both lower prices to private payers and more of the other activities. […]
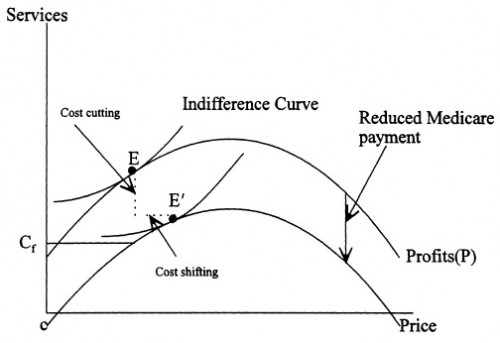
The equilibrium is for the hospital to choose point E, where it earns some profits from privately insured patients but does not charge the profit-maximizing price.
Point E is simultaneously on the profit function and the indifference curve. The latter traces out the set of service-price pairs for which the hospital is equally content to provide: they have equal utility (which the hospital seeks to maximize). Points on the indifference curve are consistent with the fact that the hospital is willing to give up provision of some services (which include unprofitable activities) if it can charge prices that are sufficiently low (because it also views lower prices as a form of “charity”). Point E maximizes utility within the feasible set of service-price pairs.
The effect of a reduction in Medicare payments is shown in the figure immediately below.
[It] can be represented as a shift down of the profit curve. The utility maximizing hospital will both reduce its “charity” care to private patients (that is, increase the prices it charges them) and reduce its profits. With the general utility function, both of these responses would occur. The effect of Medicare payment reductions on increasing prices to private patients is termed cost shifting. The effect of payment reductions on reduced profits, and thus the ability of the hospital to pursue its other missions, is termed cost cutting.
How much of the reduction in Medicare payments will show up as cost cutting and how much as cost shifting? Theory can’t tell us, but it can reveal the important criteria.
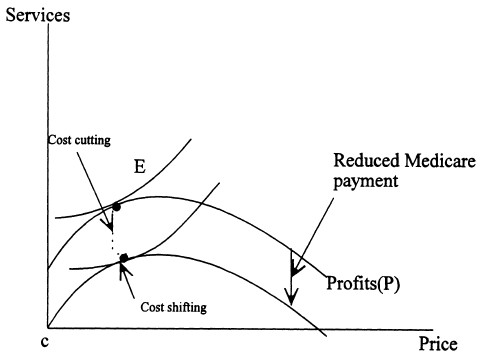
The ability to cost-shift depends on having a residual private sector where demand for hospital care is relatively inelastic. Recent [circa 1998] changes in the medical care marketplace in particular the rise of managed care have likely changed the demand elasticity. While managed care has many effects on the medical care system, the most important effect for this analysis is that it makes patients more responsive to price increases at particular hospitals.
If patients (or the plans that represent them) are more responsive to price, hospitals have less ability to shift costs. This is shown in the next figure in which
[t]he profit schedule both has a lower peak (because maximum profits are smaller) and is flatter (because the same increase in price will result in a smaller increase in profits). […] Medicare cuts in this market will result in more cost cutting and less cost shifting than Medicare cuts in the market with less elastic demand. The reason for this is that the increased demand elasticity raises the [utility] loss to the hospital of shifting a dollar of costs relative to the [utility] loss to the hospital from having lower profits. Indeed, as managed care spreads and the hospital extracts all of the revenues possible from private insurers, the entire amount of Medicare reduction will result in cost cutting. Cost shifting should be less prevalent in markets where managed care is more important.
This is the critical point. For hospitals that do not maximize profit, cost shifting can occur, but still may not be a large phenomenon. It depends on the ability of private purchasers to resist price increases, i.e., their market clout or price elasticity. In fact, once a hospital has exercised whatever market power it possesses–its ability to increase private prices without harming profit from that sector–there is no further scope for cost shifting. If a hospital, having reached that point, continued to cost shift it would reduce its flow of resources it seeks to use for its non-profit functions. Even charity care requires resources and there’s a maximum private price beyond which those resources begin to shrink.
So, how much cost shifting vs. cost cutting should we expect? Tomorrow I’ll tell you.