This is the second post on the prospects for getting causal estimates of treatment effects from observational data. The first post discusses the problems with randomized clinical trials (RCTs).
Here’s the problem with observational data and simply comparing people who have been treated with drug X to those who have gotten drug Y. The X people are probably different from the Y people in systematic ways. There are usually reasons why they got different drugs. So the observed differences in outcomes between X drug and Y drug patients might be due to unobserved differences between these patients, rather than the drugs.
Now, as Austin has explained, there are some observational data sets that can give us causal information when analyzed with the proper techniques. We can make causal inferences when there is an ‘experiment of nature.’ That is, patients either got or did not get a treatment for reasons unconnected to their illness or its course, as if they had been randomly assigned.
Unfortunately, experiments of nature are rare. So it would be great if we could extract causal information from observational data even when we do not have an experiment of nature.
In principle, however, we could get around the unobserved differences problem if we could measure enough of the relevant differences between the groups of patients. Then we could, for example, closely match drug X and drug Y patients. If we matched them on all the factors that determine who gets what treatment, then it would be as if a matched X and Y patients had been randomly assigned to get either X or Y. Then by averaging the differences between X patients and Y patients within matches, we could get an estimate of the causal effect of drug X relative to drug Y. Propensity score methods (described here by Austin) are the technique du jour for this. (There are other methods in play, but let’s stick with this idea.)
Here’s where the ‘big data’ movement comes in. We can assemble data sets with large numbers of patients from electronic health records (EHRs). Moreover, EHRs contain myriad demographic and clinical facts about these patients. It is proposed that with these large and rich data sets, we can match drug X and drug Y patients on clinically relevant variables sufficiently closely that the causal estimate of the difference between the effects of drug X and drug Y in the matched observational cohort would be similar to the estimate we would get if we had run an RCT.
If we can get treatment effect estimates from matched observational cohorts, they’ll be cheaper than RCTs. Moreover, we’ll have these estimates for the actual populations of patients who are routinely treated with these drugs, not the selected groups seen in RCTs. Researchers like Longhurst or Sebastian Schneeweiss even hope that these comparisons could be automated, so that novel questions arising in clinical care could be answered in real time. In that way, complex clinical decisions could be routinely informed by best evidence.
It’s a breathtaking idea. And it works in principle if you have measured enough of the relevant variables about how drug X patients differ from drug Y patients. But that’s a big if.
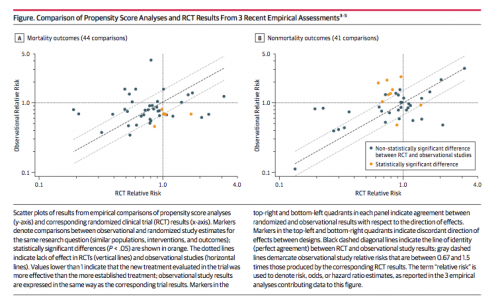
So, does causal inference from observational cohorts work in practice? Issa J. Dahabreh and David Kent summarize studies in which researchers have been able to directly compare the causal inferences about the comparative effectiveness of treatments derived from RCTs and causal inferences on the same issues derived from observational data.
In each graph, the horizontal axis shows a causal effect estimated from an RCT. Relative Risk > 1.0 mean that patients are better off with the novel treatment, < 1.0 means that they are better off with the comparator, and Relative Risk = 1.0 means there is no difference. The vertical axis shows the same causal effect estimated from observational data analyzed using propensity score matching. If RCTs and observational analyses led to identical causal inferences, the dots would fall on the dashed diagonal line. There is an association in this figure, which is great, but it’s loose. And sometimes the dots fall in the off-diagonal quadrants of the graphs, meaning that the two approaches came to opposing conclusions about which treatment is better. Dahabreh and Kent conclude that
Currently available evidence suggests that inferences about comparative effectiveness from observational data sometimes disagree with the results of RCTs, even when contemporary methods of confounding control are used.
In other words, causal inferences from observational cohorts aren’t fully reliably yet, possibly because we aren’t measuring the right variables.
That doesn’t mean it will never work. Dahabreh and Kent comment that
What remains unknown is how much coupling advanced statistical methods with more and richer “real-life” data will improve the validity of study results and what the determinants that identify study validity are.
It’s early days in the construction of large data sets from EHRs, meaning that the empirical agreement between causal estimates from RCTs and observational cohorts may improve. Moreover, if you do not have RCT evidence or an experiment of nature, then cautious use of the best observational evidence may be better than nothing.