The relative strengths and weaknesses of randomized clinical trials (RCTs) and observational studies is a frequent theme at TIE (e.g., here and here). RCTs are great because they do a good job of identifying the causal effect of a treatment. Observational studies can be great too, particularly if they are based on strong non-experimental designs.
Now suppose that we have both RCTs and observational studies on the effectiveness of a treatment and they show varying results. How do you put together evidence from both kinds of studies to come up with a unified view of the effectiveness of a treatment?
This is the question that Ely Kaizar takes up in the Annual Review of Statistics and Its Application.
Although both randomized and nonrandomized study data relevant to a question of treatment efficacy are often available and separately analyzed, these data are rarely formally combined in a single analysis. One possible reason for this is the apparent or feared disagreement of effect estimates across designs, which can be attributed both to differences in estimand definition and to analyses that may produce biased estimators. This article reviews specific models and general frameworks that aim to harmonize analyses from the two designs and combine them via a single analysis that ideally exploits the relative strengths of each design. The development of such methods is still in its infancy, and examples of applications with joint analyses are rare.
Kaizar’s approach extends ideas from meta-analysis. The goal of a meta-analysis is to combine the results of many clinical trials to derive an overall estimate of the treatment effect. That estimate is a number: for example, a meta-analysis of the effect of a new statin might present an estimate of the difference in the percentage reduction of cholesterol achieved if you take the new drug compared to the percentage if you take Lipitor.
However, we may want to find out more from a meta-analysis. In particular, we may think that the effect of our treatment is not a one-size-fits-all phenomenon, but rather that the magnitude of the effect varies based on a patient factor, for example, whether the patient has a particular genetic allele. If so, what we want to estimate is not just a number but rather a function describing how the treatment effect varies across patients’ genomes. Meta-analyses of this kind assume that we have access not just to summary statistics from individual studies but also to the individual patient-level data.
Unfortunately, we’re unlikely to find collections of RCTs that capture the diversity of patients in the real world. We might, however, be able to find observational data sets that more closely capture the diversity of actual patient populations. Kaizar’s goal is to combine both types of data in a single analysis, so that we can have an internally valid estimate of the causal effect of treatment (the RCT’s strength) and the generalizability of the results to real patient populations (the strength of observational designs).
So now we want to look not just at how the treatment effect varies as a function of patient factors, but also as a function of the study methodology. The Figure below summarizes the results of a hypothetical joint analysis that pools patient data from both randomized and non-randomized studies.
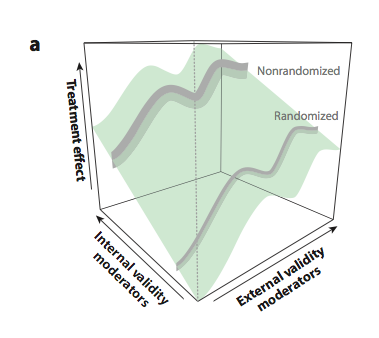
The treatment effect is a surface because the estimated magnitude of the effect varies depending on the patient population being studied (“external validity moderators”) and the methodology of the study (“internal validity moderators”).
To date there are very few examples of joint analyses of RCT and observational data (here’s one from a group including Kaizar [and me]). Why are there so few applications of these ideas? One reason is that, as Kaizar acknowledges, there are many methodological questions to be answered about how to jointly analyze RCT and observational data.
The larger problem is that there are few domains where we have access to individual level data from both RCTs and observational studies, and in which these studies measure enough of the same variables in similar ways to permit the data to be pooled.
Nevertheless, it’s possible that in a future world of learning health care systems, health care organizations will routinely collect data on treatments and their outcomes. Moreover, in a future world of open science, data from clinical trials might be routinely archived for reuse. If so, we will have more data sets from diverse populations gathered in both RCT and observational studies.
Learning how the effect of treatment varies across patients is the essential task of precision medicine. Methods such as those reviewed by Kaizar may be vital to its success.

