There are many potential medical applications of machine learning, such as reading radiological images. But despite decades of effort, machine learning has found fewer applications in medicine than in many other fields. Is this about to change? Machine learning is transforming many technology applications and attracting large investments from Amazon, Apple, Facebook, Google, and Microsoft. So I’ve been trying to figure out what machine learning is and how it works. That led me to a remarkable paper.
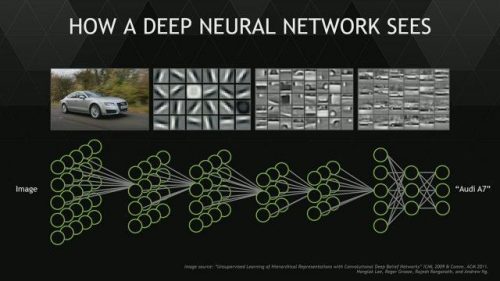
The deep learning algorithm is a machine learning technology that enables computers to classify images by learning from example data. The key idea is that input data (e.g., the matrix of pixels that comprise the photo of the Audi on the left) are processed through a hierarchical chain of linear and non-linear transformations. Each transformation (or layer) is implemented as a neural network. Each layer takes the output of the previous layer as input, finds structure in it, and passes the results as output to the next layer. The final output is a classification of the original image (“Audi A7”). The Google Tensor Flow project documents the impressive recent progress in deep learning: error rates on a benchmark task have fallen by a factor of five in the last four years.
The paper in question is about why deep learning works. Henry Lin, who seems to be an undergraduate prodigy, and Max Tegmark, a well-known theoretical physicist (hereafter, L & T), argue that deep learning works not only because it is a powerful algorithm, but also because the world, seen at a high level of abstraction, is simple, and hence learnable.
We show how the success of deep learning depends not only on mathematics but also on physics: although well-known mathematical theorems guarantee that neural networks can approximate arbitrary functions well, the class of functions of practical interest can be approximated through “cheap learning” with exponentially fewer parameters than generic ones, because they have simplifying properties tracing back to the laws of physics. The exceptional simplicity of physics-based functions hinges on properties such as symmetry, locality, compositionality and polynomial log-probability, and we explore how these properties translate into exceptionally simple neural networks…
Why is it surprising that deep learning works? An image classification application is a function that maps complex data (e.g., a dense grid of pixels) to a category (a particular brand of car). Constructing such a function (“training” the machine learner) is essentially a curve fitting exercise. In math, how to fit a curve to a highly complex functions is a solved problem. But what the math shows is that you can approximate a complex function as accurately as you like, given indefinitely large amounts of data and unlimited time. But an algorithm that doesn’t converge to a solution before the Sun explodes won’t replace a radiologist. The computer science problem, therefore, is to find a computationally feasible technology. Deep learning models are simple enough that you can train them in a reasonable amount of time, and yet they solve challenging image classification problems. So, how do they do that?
L & T say that deep learning works not just because the algorithm is built on clever, powerful math, but also because the physical structure of the world is simple. Moreover, the world is simple in a way that is mirrored by the structure of the algorithm.
To me, the claim that ‘the world is simple’ is what stand-up humour must be like on the planet Vulcan. L & T remark that
For reasons that are still not fully understood, our universe can be accurately described by polynomial Hamiltonians of low order d.
That line just kills, no? The claim seems absurd: if you’ve studied molecular biology, you weren’t staggered by the simplicity of the world. But L & T’s point is that if you look up the famous eponymous equations (Maxwell’s, etc.), the ones that drive the world, they are often strikingly simple. This may not be an accident.
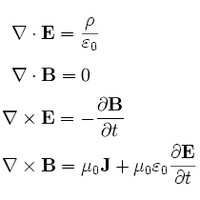
As a commenter on the L & T paper noted,
These properties of the… Hamiltonian[s] appear necessary in order for the world to “work”: to be described by equations of motion or, equivalently, field equations that have mathematically stable, robust solutions.
In other words, if these fundamental laws were more complicated, the transitions of the world from one state to the next would be chaotic. Stuff would blow up.
L & T also identify several other physical features of the world that make things simple. For each such feature, they argue that it is mirrored by a feature of the mathematics of deep learning. The most important of these features is the hierarchical structure of compositionally, which is mirrored by the layers of deep learning.
One of the most striking features of the physical world is its hierarchical structure. Spatially, it is an object hierarchy: elementary particles form atoms which in turn form molecules, cells, organisms, planets, solar systems, galaxies, etc. Causally, complex structures are frequently created through a distinct sequence of simpler steps.
The cool thing about this hierarchy — that big things are composed of little things that are composed of yet littler things — is that it makes human learning a lot easier. To understand what happens at one scale, you need to know about the littler stuff one level down that your objects are composed of. To understand cell biology, you need to know some biochemistry. But you don’t have to master the entire stack: quantum mechanics not required. L & T argue that the compositional hierarchy simplifies learning for machines too.* That is, deep learning works because the layers of networks mirror the compositional hierarchy in that each successive layer condenses the information that was output from the previous layer.** The deep learning algorithm can concentrate its effort on one part of the problem at a time, rather than thinking about everything at once.
So L & T’s argument is that: (1) The world has a physical architecture that is isomorphic to the mathematical architecture of deep learning. (2) Deep learning works when (and because) it finds this hierarchy and exploits the underlying simplicity to reduce the burden of computation.
This suggests that deep learning represents a breakthrough in our ability to make machines that can perceive what we perceive. Even if that’s true, that doesn’t mean that deep learning can endow machines with human intelligence. We can do a lot more than process light on our retinas into percepts like “Audi 7”. We can also prove theorems. But it’s not obvious to me how a deep learner could carry out a logical deduction; and that’s just one example of what we can do. But who cares? If deep learning represents a tipping point in progress toward mechanized perception, it will lead to significant advances in many areas of medicine.
I’m also struck that L & T may have uncovered something about why we are so at home in the world. By “at home”, I mean that we have minds that seemingly effortlessly project a world of objects that are “at hand” for our understanding and use. Our brains are much more complex than the deep learning algorithm, but they too can be described as layers of neural networks. If so, perhaps we are at home in the world because we too mirror the world’s physical architecture.
*L & T are not saying that deep learning identifies an Audi by first recognizing molecules of steel and glass and then moving up. It’s just an analogy. As the figure at the top suggests, the algorithm decomposes images into features, but aren’t the same hierarchy of features as the canonical physical hierarchy that L & T reference. It’s not clear to me whether this is a significant weakness in their argument.
** That is, each layer calculates and outputs sufficient statistics that summarize the essential features of the inputs to the layer, with minimal loss of useful information.

