Of the 60 tallest buildings in the world select one. Guess the first digit in the number expressing its height in feet. What’s the best guess, the most likely digit? Curiously enough the answer has a unique solution: the number 1 is the most likely. It seems odd, even wrong, that the probability is not uniform over the nine possible digits. That it isn’t is Benford’s Law, a curious number-theoretic result with application in fraud detection.
Of course Benford’s Law has a mathematical proof (here’s another), but I’ll avoid that and lean on an intuitive example from Wikipedia.
[I]f a quantity doubles every year, then it will be twice its original value after one year, four times its original value after two years, eight times its original value after three years, and so on. When a quantity which doubles every year reaches a value of 100, the value will have a leading digit of 1 for a year. In the next year, the value rises from 200 to 400 and will have a leading digit of 2 for a little over seven months, and 3 for the remaining five months. In the third year, the leading digit will pass through 4, 5, 6, and 7, spending less and less time with each succeeding digit. Early in the fourth year, the leading digit will pass through 8 and 9. When the quantity’s value reaches 1000, the process starts again. From this example, it can be seen that if the value is sampled at uniformly distributed random times throughout those years, it is more likely to be measured when the leading digit is 1, and successively less likely to be measured with higher leading digits.
This example makes it plausible that data tables that involve measurements of exponentially growing quantities will agree with Benford’s Law. But the law also appears to hold for many cases where an exponential growth pattern is not obvious.
The height of buildings would be one such non-obvious case where Benford’s Law appears to hold.
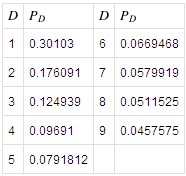
The following table from Wolfram MathWorld provides the probability distribution predicted by Benford’s Law. Notice that the digit 1 is the most probable and each subsequent digit is less likely.
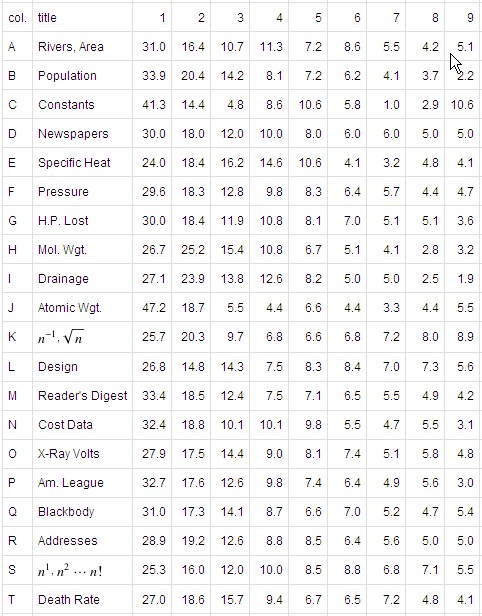
But that’s theory. Here are some empirical results, also from Wolfram MathWorld (entries in the body of the table are empirically determined percentages):
Benford’s Law has been applied to law enforcement in the areas of forensic accounting and fraud detection. If you’re cooking the books by making entries according to a distribution other than the one given by Benford’s Law you may be far more likely to get caught. Had Bernie Madoff investors used Benford’s Law to check his work they might have discovered something fishy.