Joshua Angrist has many papers explaining and using instrumental variables (IV). In a 2001 Journal of Economic Perspectives (JEP) article with Alan Krueger he digs into IV’s history and provides some intuition for the method (official and ungated versions).
According to Angrist and Krueger, P.G. Wright (1928) deserves credit for the first use of IV in estimating supply and demand elasticities of flaxseed. But, “Wright’s econometric advance went unnoticed by the subsequent literature. Not until the 1940s were instrumental variables and related methods rediscovered and extended.” In 1953 Theil developed two-stage least squares, the most common way to implement IV estimation.
The rest, as one might say, is history. Only it took a long time for IV approaches to gain serious traction in many areas of applied economics. They’ve been widely used in labor economics for at least two decades, became popular in industrial organization in the last 15 years or so, and have had very little use in health services research. The increased use, where it has occurred, corresponds to greater availability of data and computational resources.
Data and computer power exist in health services research as they do in labor or IO. So why has diffusion been slow in that field? Three reasons: (1) Randomized trials are often possible and they “crowd out” other modes of inquiry. (2) Economists are sparse in the field. And (3), the intuition of IV has not been successfully communicated to non-economist practitioners.
An intuitive application of IV is found in Angrist’s and Krueger’s 1991 paper on the effect of school attendance on earnings, which the authors review in their JEP article. One might hypothesize that earnings are causally related to years of schooling. More school translates into higher pay. But the possibility exists that there are unobservable factors that relate to both time in school and earnings, like motivation and innate skill. Therefore, a naive estimation of the effect of earnings on years of education would produce biased results.
A feature of state law provides an opportunity to avoid such bias. Most states require students to begin school the calendar year they turn six. They also require students to stay in school until age 16. With a cutoff of December 31, children born in the final quarter of the year begin school in September at about age 5.75. Those born in the first quarter of the year begin school in September at about age 6.75.
Some subset of the population will quit school at age 16. By a student’s 16th birthday, she has had a number of years of schooling related to her month (or quarter) of birth. Angrist and Krueger make the crucial observation that “[b]ecause an individual’s date of birth is probably unrelated to the person’s innate ability, motivation or family connections (ruling out astrological effects), date of birth should provide a valid instrument for [length of] schooling.” That is, individuals are, in part, randomized by birth date to length of schooling (most obviously, those that quit at age 16, though likely others as well).
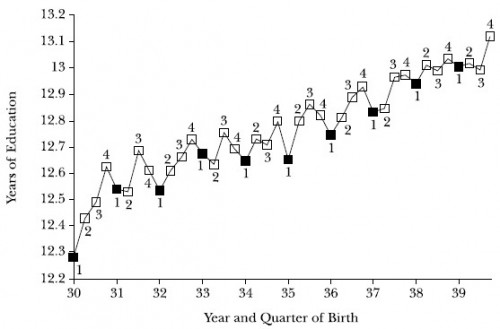
The figure below, reproduced from Angrist’s and Krueger’s JEP article, illustrates the relationship between years of education and quarter of birth for the cohort born in the 1930s (1 = first quarter, 2 = second quarter, etc.). In addition to quarter of birth, year of birth is also a factor, one that is easy to control for since it is observable.
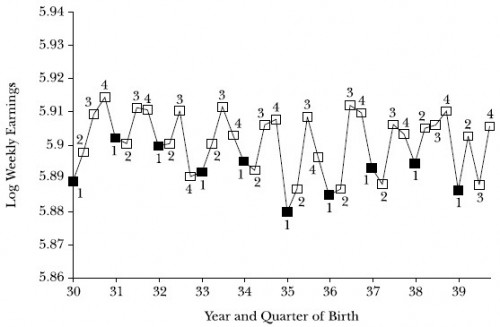
The following figure reveals that those born in early quarters of the years in the 1930s tend to earn less in 1980 than those born in later quarters. Using quarter of birth as an instrument for length of schooling (while controlling for other observable factors of relevance), permits one to obtain an unbiased estimate of the effect on earnings of duration of schooling.
If one accepts that birth date is unrelated to earnings except through its affect on years of school, the use of birth date as an instrument for years of school is essentially equivalent to a randomized trial. What are the chances one can actually randomize students to years of schooling and then find them about 50 years later to measure their earnings? Not large. Hence, this example illustrates how to obtain results equivalent to those of a randomized trial in a circumstance in which one is unlikely to occur.
References
Angrist, Joshua D. and Alan B. Krueger. 1991. “Does Compulsory School Attendance Affect
Schooling and Earnings?” Quarterly Journal of Economics. November, 106:4, pp. 979–1014.
Theil, H. 1953. “Repeated Least Squares Applied to Complete Equation Systems.” The Hague: Central Planning Bureau.
Wright, Phillip G. 1928. The Tariff on Animal and Vegetable Oils. New York: MacMillan.