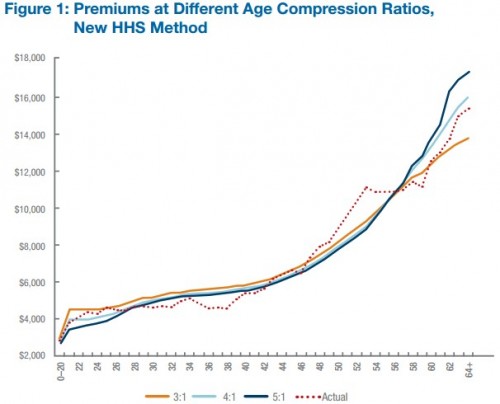
I linked to the this work by Blumberg and Buettgens earlier in the week, but I can never trust more than 2% of you to click through, let alone read the document. It’s analysis of the effect of age rating on net premiums (accounting for subsidies) in health insurance exchanges. What it shows is that the 3:1 constraint in current law (that older consumers’ premiums can’t be more than three times those of younger consumers) isn’t significantly binding, on average. It doesn’t actually do a lot to constrain older people’s premiums or increase younger people’s very much. Consequently, loosening up this regulation wouldn’t do a lot. Compare the orange line (3:1 age band-based) with the dotted line (actual premiums) in the chart below. (Curves are jumpy because they are based on a simulation of a finite number of consumers.)
UPDATE: Post edited to reflect the fact that what is shown is premiums, net subsidies, on average. Also, a relevant follow-up post is here. Read that follow-up if you think this chart is contradicting what you think you know from the rate shock debate.