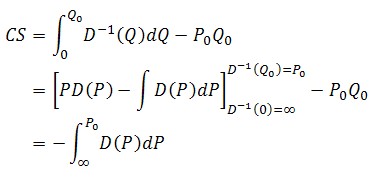Why Consumer Surplus is Negative the Integral of the Demand Function

Having just spent too many hours on this, I’m posting it so I won’t forget it. Maybe it’ll save some other folks some time too.

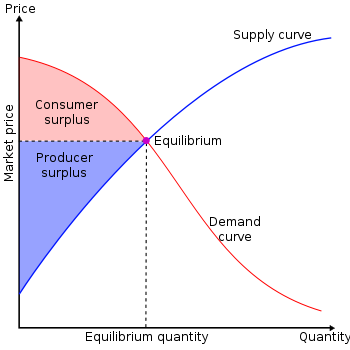
I’ve learned that, up to a constant, consumer surplus is the integral of the demand function. That’s wrong. It’s negative the integral of the demand function. The reason has to do with the fact that what we call the demand function–that which translates price into quantity–is not what we draw on a graph. Thanks to Alfred Marshall, the custom is to draw the inverse demand function, with price on the vertical axis and quantity on the horizontal axis.

To show formally that consumer surplus is the negative of the integral of demand (or that demand is negative the derivative of consumer surplus), one can use the rule for integrating inverses. To do so, let

• Q denote quantity and P denote price,
• Q = D(P) be the demand function,
• and the equilibrium quantity and price be Q₀ and P₀, respectively.

Then, consumer surplus (CS) is

where the first line is the definition of consumer surplus, the second follows from the rule of integrating inverses and the facts that Q=D(P) and P=D^-1(Q), and the third holds if PD(P) is zero when P is infinity.

This is important for the very reason I spent hours trying to find or work out the above explanation. If one is working with discrete choice models (logit, nested logit, conditional logit, etc.) and wishes to derive the expression for consumer surplus, one might do so by recalling two things:

1. The functional form of consumer surplus is the log of the denominator of the discrete choice probability model, which is also the demand function. That is, consumer surplus has a log-sum of exponentials form.
2. The derivative of consumer surplus is negative the demand function, i.e. the discrete choice model.

Recalling point 1 and not 2, which is what I did, one is tempted to put the wrong sign on consumer surplus. That leads to very incorrect (exactly backwards) results. One is tempted to scrutinize one’s code for bugs. But the problem isn’t the code, it’s Alfred Marshall’s graphing convention.