Alex Tabarrok proposed a problem similar to one proposed to me in college. You can read his problem on his blog. Below I state mine, which you can also find elsewhere on the internet. I kept my notes on how to solve it which I also include below (don’t peek if you want to try to solve the problem on your own).
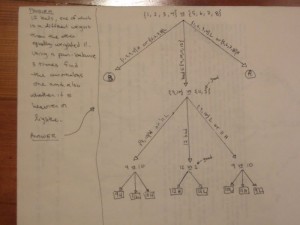
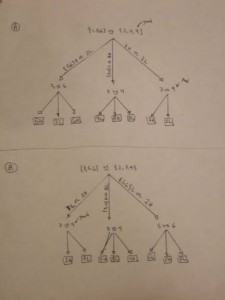
Problem: There are 12 balls, one of which is a different weight than the other equally-weighted eleven balls. Using a pan balance three times find the anomalous ball and also whether it is heavier or lighter than each of the others.
There are no tricks or gimmicks. This is an honest problem. It can be solved. Below is my solution. I think (hope) my notation is self-explanatory.
Solution: (Click to enlarge photos. If it is still too small use the magnifying glass icon in the upper right on the referred page.)