Alan Krueger and Ilyana Kuziemko collaborated with Gallup to augment one of their representative surveys that includes questions on health insurance coverage. They worked in additional questions to elicit individuals’ willingness to pay for coverage. The key survey question was, “If you could get a health insurance policy for yourself that is as good as the one that members of Congress have, given your current financial situation, would you buy it for $X a year, which works out to $X/12 per month?” Their findings appear in a recent NBER working paper.
[W]e estimate that about sixty percent of the uninsured would voluntarily enroll for an annual premium of $2,000. Under the current specification of subsidies in the ACA, we estimate that over 75 percent of uninsured adults would enroll, implying that some 39 million uninsured individuals would gain coverage as a result of the law. We also estimate that stripping the individual mandate from the law […] would lead to between 7 and 12 million fewer individuals gaining coverage.
The Gallup data included extensive information on health status, and thus allow us to gauge the extent of adverse selection for a given subsidy schedule. […W]e find no evidence that less healthy individuals would be more likely to enroll, with or without a mandate. […]
[W]e estimate higher take-up rates under the provisions of the ACA than does the Congressional Budget Office. (Bold mine.)
If the purpose of the mandate is to mitigate adverse selection, this study suggests it isn’t necessary. It is still significant that fewer would be covered without a mandate, but without an adverse selection externality, the strongest argument of the mandate evaporates. (I never take one study as definitive evidence of anything. Notably, at least one other study provides evidence consistent with the view that a mandate is necessary for selection reasons.)
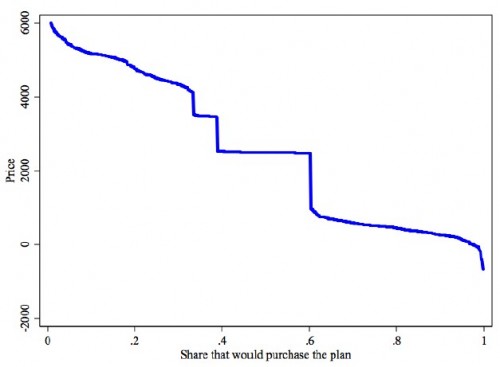
Here’s Krueger’s and Kuziemko’s estimated demand curve. As expected, it is broadly downward sloping, but with bunching at certain prices.
UPDATE: Included the survey question.