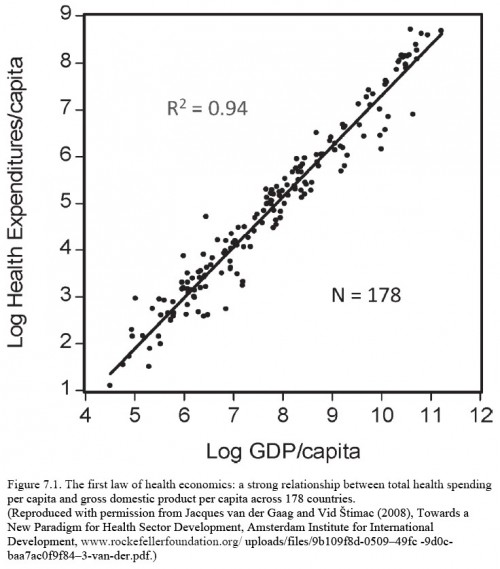
Chapter 7 of The Cost Disease can be summed up with the fact that the elasticity of health care with respect to wealth is greater than one, the hallmark of a luxury good. Translation: we tend to spend a greater proportion of our wealth on health as our wealth increases. This gives rise to charts like the one Baumol shows in the chapter for nations at a point in time:
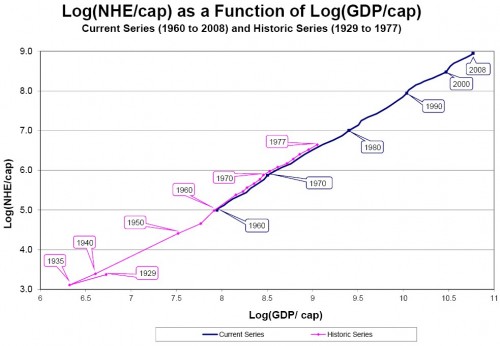
We have seen something similar in the U.S. over time:
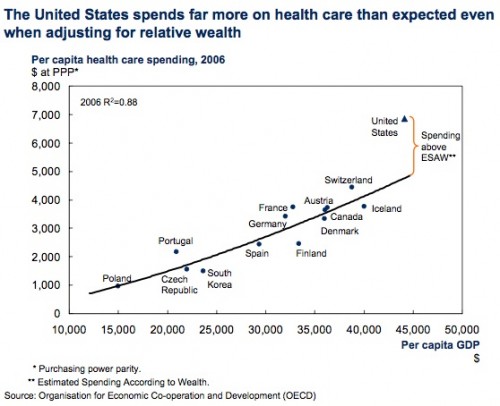
However, the U.S. is still an outlier in the sense that we spend more than one would expect considering wealth alone:
It should be noted that all of the above pertains to spending not cost. The former is price times quantity (p x q), summed over the various services and products in the health sector; it’s an economic measure of the output of health care consumed. The later is a measure of the resources required to produce those services and products, i.e., it’s an economic measure of the inputs to the production of health care. Cost and spending are not the same thing because inputs and outputs are not the same thing.
Let’s turn to Chapter 8, about which I have little to say. It makes the point that sectors have different rates of change in productivity, due to their mix of inputs. Some inputs are inherently stagnant, like human ingenuity, while others exhibit rapid increases in productivity, like computer resources. Baumol provides several examples of mixtures of stagnant and progressive inputs, including R&D.
Being a researcher, I can attest to some of the changes in productivity over the last 20 years or so. One thing I’ve observed is that as computational resources have become cheaper, it has been possible to do more work with fewer person-hours input. For instance, I require fewer hours of clerical and programmer support to do the same type of work. This is a replacement of stagnant inputs for progressive ones, a change in the mixture of inputs. To be sure, there may be a limit to the extent the mix can change, but until the limit is reached the cost disease may be ameliorated.
All posts about the book are under the Cost Disease tag.