The following is a guest post by Matthew Martin, a health economist and programmer for the Cancer and Blood Diseases Institute at Cincinnati Children’s Hospital Medical Center. He researches the economics of sickle cell and pediatric hematology, as well as applying mechanism design and reduced form causal inference methods to problems in health care. He earned his master’s degree in economics from Cornell University in 2013, and blogs about economics at Separating Hyperplanes.
Studies suggest that if the ACA subsidies are repealed, as the plaintiffs in King v Burwell seek to do for states that did not set up their own exchanges, then the pre-subsidy premiums for insurance plans on the ACA exchanges would increase dramatically. If you are unfamiliar with the concept of adverse selection, this may surprise you because we normally think of subsidies as increasing pre-subsidy prices due to increased demand. What gives?
Einav and Finklestein (2011) laid out the textbook approach to analyzing adverse selection, using graphical methods to illustrate the theory.
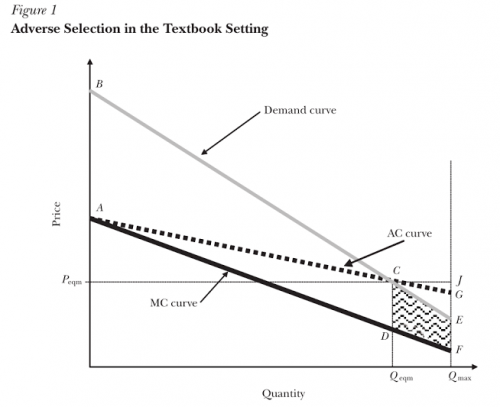
We can think of consumers in this market as deciding whether or not to buy a health insurance policy, although the same analysis applies to the decision between more versus less coverage. Each point on the marginal cost (MC) curve represents the expected health costs of an individual consumer in the market, plus some extra amount to cover additional “loading costs” such as the insurer’s administrative costs and markups, while the corresponding point on the demand curve shows the individual’s willingness to pay for this insurance plan. Because they are risk-averse, the demand curve will exceed the marginal cost for most people–they would prefer to pay a little bit more every month than suffer the chance of a rare but catastrophic medical bill. Thus, so long as loading costs remain smaller than this risk premium for everyone, having insurance makes everyone better off. Graphically, this means that the Pareto Efficient level of coverage is where everyone for whom demand exceeds marginal cost has coverage.
If insurers could charge everyone a premium equal to their marginal cost, as was the goal in this proposal which TIE weighed in on previously, we’d end up with the efficient level of coverage.
However, insurers often cannot charge different premiums to individuals with different marginal costs for a variety of reasons, especially now that the ACA prohibits most forms of risk-rating. But even before the ACA, most studies found adverse selection in risk-rated markets, suggesting insurers could not perfectly differentiate healthier from less healthy individuals due of asymmetric information. For a modern take on the implications of asymmetric information for adverse selection, see Koch (2014). Together, this means that with few exceptions, insurers must charge everyone the same premium, and that premium must be high enough to cover their average expected costs, illustrated by the AC curve in the graph. Note the wedge between the AC and MC curves, which arises because the average decreases more slowly than marginal cost.
Because the demand curve represents individuals’ willingness to pay insurance, the intersection between demand and the AC curve determines the actual number of people who opt to buy insurance and the actual premium charged. Everyone to the left, for whom demand exceeds AC, buys insurance, while everyone to the right does not. Importantly, note that for many of the individuals to the right of this point the demand curve nevertheless exceeds the MC curve, so that the actual cost of insuring them is still less than their willingness-to-pay! Thus with these healthier (less costly) individuals dropping out of the market, adverse selection leads to inefficiently low levels of insurance and higher insurance premiums.
A subsidy like the ones offered on the ACA exchanges shifts the demand curve up, so that the premium at which individuals will buy insurance equals their willingness-to-pay plus the subsidy amount. This, in turn, shifts the intersection between demand and AC to the right, in the direction of more coverage and lower average cost, lowering premiums for everyone.
The classical model where subsidies increase prices relied on having an upward-sloping marginal cost curve. The forces that cause upward-sloping MC curves in most markets didn’t totally disappear for health insurance markets–we can imagine that loading costs generally increase as more people buy insurance–but they are dwarfed by the size and heterogeneity in actual healthcare expenses, producing an overall downward-sloping MC curve. Thus, when in the presence of adverse selection, subsidies not only reduce the cost of insurance to those who receive them, but to everyone in the market. There’s a simple algebraic demonstration of this result here.


