I’ve always been a fan of good survey research. Sometimes, surveys are the best way to answer simple questions. In the most recent issue of Obstetrics and Gynecology, there’s a good example of such a study:
OBJECTIVE: To estimate prevalence and correlates of abortion provision among practicing obstetrician–gynecologists (ob-gyns) in the United States.
METHODS: We conducted a national probability sample mail survey of 1,800 practicing ob-gyns. Key variables included whether respondents ever encountered patients seeking abortions in their practice and whether they provided abortion services. Correlates of providing abortion included physician demographic characteristics, religious affiliation, religiosity, and the religious affiliation of the facility in which a physician primarily practices.
A survey of 1800 ob-gyns is a large sample. The response rate was 66%, which is pretty impressive for a survey of physicians. It didn’t hurt that they were offering a $20 inducement with the first survey. They also offerred an additional $30 to potential respondents with the third mailing. On a side note, that was an odd thing to do, because it actually tempts participants not to respond to early mailings. But they did fine. This was not a cheap survey to do.
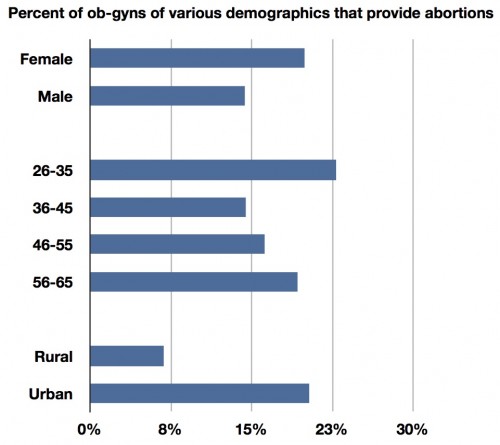
A whopping 97% of practicing ob-gyns had encountered patients seeking abortion, yet only 14% of ob-gyns perform them. That’s significantly fewer than previously thought. The study also provides some interesting data on which ob-gyns are more likely to provide abortions. Here’s a chart I made with their data:
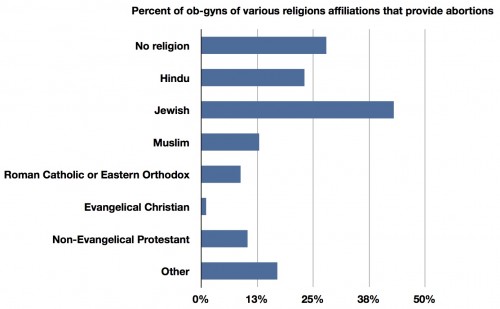
Male ob-gyns are less likely to provide abortions, as are middle-age ones. If you live in a rural area, you’re very unlikely to find an ob-gyn who will provide an abortion. And here’s some religious data:
Almost no Evangelical Christian ob-gyns will provide abortions. Jewish ob-gyns are the most likely to provide abortions, even more likely than ob-gyns who report having no religion at all. This study doesn’t prove causality, so we can’t tell if any of these factors cause providers to provide abortions or not, but it’s interesting nonetheless.