A Bit More on Physical Pendulum Isochronal Pivot Points

This is a follow-up post to this one, which you should (re)read if this topic is of interest to you and any of the following is unfamiliar. The same warning about mobile viewing applies: all square roots are over both numerator and denominator, despite how it may appear on a mobile device.

A physical pendulum with mass m and center of mass (CM) moment of inertia I_cm pivoting at a point d from the CM has period T given by

$$T = 2\pi \sqrt{\frac{I_{\text{cm}} + md^2}{mgd}}$$

with g being the acceleration due to gravity. The last post showed that T has the same value on two circles centered on the pendulum’s CM, one with radius d and one with radius d’, where d’ = L – d and

$$L=\frac{I}{md}$$

Here I = I_cm+ md². The CM-centered circles of radius d and d’ are composed of isochronal points. That is, the period is the same no matter which point on these circles the pendulum is pivoted about.

This post explores T as a function of d (or d’) and some properties of d.

How T Behaves as d Varies

T as a function of d has a shape as shown in the figure below, where the horizontal and vertical axes represent d and T, respectively.

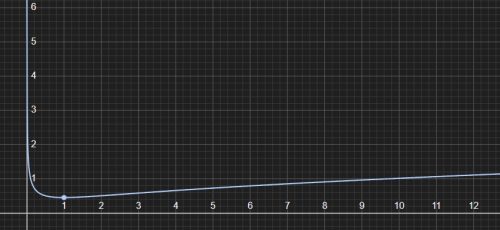
This suggests T approaches infinity as d approaches zero or infinity. This can be shown formally by taking limits, but it’s not hard to see informally by examining the expression for T.

As d approaches zero, the expression for T resembles (or behaves like) a constant times the inverse of the square root of d, which is asymptotic to the T-axis in the above plot and certainly goes to infinity. As d approaches infinity, the expression for T behaves like a constant times the square root of d, which also goes to infinity, as the graph shows.

This behavior of T as d approaches zero or infinity makes sense. As d approaches zero, the pendulum’s pivot point approaches its CM. There is no restoring torque at the CM, and the pendulum would not return from a displacement. Think of turning a disk of uniform density pinned at the center (its CM). If you give it a turn, it won’t turn back. That’s an infinite period.

As d approaches infinity, the situation resembles a simple pendulum, for which the period is proportional to the square root of its length (d), hence T also approaches infinity.

Moving away from these extremes, T strictly monotonically decreases to a minimum. This itself means that the minimum must be where d=d’. If this were not the case, then there would be two isochronal circles, centered on the CM, of minimum T, one of radius d and one of radius d’. This would imply that all pivot points a distance r from the CM such that d<r<d’ have larger periods, which contradicts the strict monotonicity of T from zero (or infinity) to the minimum.

Or, we could take the derivative of T with respect to d and set it to zero (steps omitted) to find that the minimum T is where

$$d^2 = \frac{I_{\text{cm}}}{m}$$

From the previous post, this is also the expression for dd’. That means that the minimum T is found where d and d’ coincide. This value of d is also the radius of gyration. By definition, this is the radius such that if all of m resided there, the moment of inertia would be the same as the object’s (here the pendulum) with distributed mass.

Plugging this into the expression for T given above, the minimum T (or, for convenience, T²) is

$$T_{\text{min}}^2=\frac{8{\pi }^2}{g}\sqrt{\frac{I_{\text{cm}}}{m}}$$

So, when d=0, d’=∞ we have two (degenerate) isochronal circles for which T is infinite. As d moves radially outward from the CM, d’ moves inward, and the circles they define are always composed of isochronal points. As this happens, T drops from infinity toward a unique minimum proportional to the quartic root of I_cm/m. The minimum is achieved when d=d’, at the radius of gyration, and the two isochronal circles become one (♥ cue violins ♥).

Where is the Minimum with Respect to the Pendulum?

Where is the d for which T is minimum with respect to the boundary of the pendulum? It’s never outside the boundary of the pendulum. I’ll show this mathematically, below, but it’s intuitive. Lengthening a simple pendulum, for which all the mass is at the end of the (assumed massless) support, increases its period. So, it stands to reason that a pivot point beyond the surface of a physical pendulum would have a larger period than a pivot point on its surface. Also, the definition of radius of gyration makes it pretty clear that it’s within the pendulum.

Let’s do it with math anyway. The pendulum’s CM rotational inertia is, by definition

$$I_{\text{cm}} = \int r^2 \, dm$$

where r is the perpendicular distance from the CM to a infinitesimal mass element dm. Replacing r with r_max, the largest distance from the CM to the boundary of the pendulum, we get the inequality

$$I_{\text{cm}} = \int r^2 \, dm \leq r_{\text{max}}^2 \int dm$$

Or, simply,

$$I_{\text{cm}} \leq r_{\text{max}}^2 \, m$$

Substituting this into the expression for the T-minimizing d above, d ≤ r_max. Equality is obtained only when all the pendulum’s mass is at a constant radius from the CM (an idealized hoop of zero width). Otherwise, the T-minimizing d is strictly within the pendulum’s boundary. For all practical purposes (assuming there are any), d < r_max. That is, not only is the T-minimizing d not outside the pendulum, it’s not even on the surface (apart from the idealized hoop). It’s somewhere strictly inside the pendulum. That means that both d and d’ are within the boundary of the pendulum for some range.

If the body of the pendulum includes the CM (true for convex shapes like a disk or triangle), then all possible values of T, from its maximum of infinity to its minimum at the d defined above are found at pivot points within it. For all such values of T, there are arcs* of one or two isochronal circles within the body of the pendulum — one when d’ is outside the pendulum’s boundary and two when it is inside, which, as noted above, it will be for some range. In fact, that range is when d’ is between the T-minimizing d (the radius of gyration) and r_max. 

If the body of the pendulum does not include the CM (as would be the case for some concave shapes like a uniform density banana or a washer), the maximum T for which a pivot point is inside the body of the pendulum is given by

$$T = 2\pi \sqrt{\frac{I_{\text{cm}} + m r_{\text{min}}^2}{m g r_{\text{min}}}}$$

where r_min is the distance from the CM to the point within the pendulum closest to it.​

Summary

• The period of a physical pendulum, T, varies with pivot point from infinity (at pivot points CM and infinity) to a minimum at the radius of gyration.
• ​A minimum achieving pivot point is always within the body of the pendulum.
• If the body of the pendulum includes the CM, then for all possible values of T, from its minimum to infinity, there are arcs of one or two isochronal circles within the body of the pendulum.​
• If the body of the pendulum does not include the CM, there are only isochronal circle arcs for T less then a finite maximum value, an expression for which we found.

* I’m talking arcs of circles and not necessarily full circles here because there may be some radial distances from the CM for which the body of the pendulum exists for only some angles. Think of a triangular-shaped pendulum as opposed to a disk-shape one. For the former, there are some CM-centered circles of radius less than the extent of the triangle that aren’t entirely within the triangle. For the latter, this is not true.