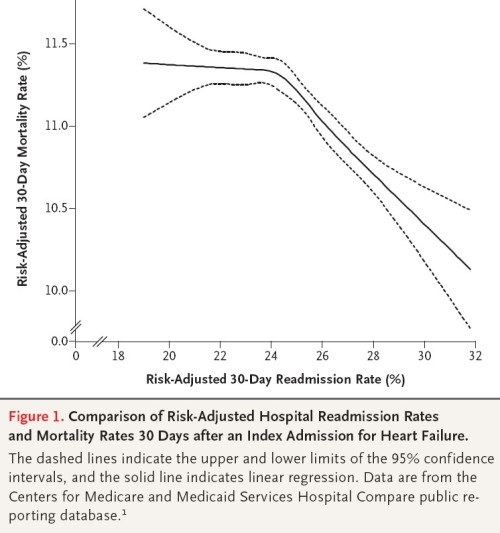
Maybe I’m not crazy. A mortality-readmission trade off has also been illustrated in a NEJM letter to the editor (lead author: Gorodeski).
We examined the association between risk adjusted readmission and risk-adjusted death within 30 days after hospitalization for heart failure among 3857 hospitals included in the CMS Hospital Compare public reporting database (www .hospitalcompare.hhs.gov) that had no missing data. We used linear regression analysis with restricted cubic splines (piecewise smoothing polynomials). […]
Our findings suggest that readmissions could be “adversely” affected by a competing risk of death — a patient who dies during the index episode of care can never be readmitted. Hence, if a hospital has a lower mortality rate, then a greater proportion of its discharged patients are eligible for readmission. As such, to some extent, a higher readmission rate may be a consequence of successful care. Furthermore, planned readmissions for procedures or surgery may represent appropriate care that decreases the risk of death.
An exceedingly blunt way to put it is, if we encourage hospitals to reduce readmission rates are we encouraging them to kill people?
UPDATE: I had suggested that this letter to the editor was peer reviewed. That may not be the case, though I do not know NEJM’s policy on this.
UPDATE 2: I’ve gotten some push-back on this by email, so let me explain a bit more of my thinking. I’m not saying that hospitals will kill people with the intention to reduce rehospitalization rates. What I’m saying is that a hospital or health system might do some things that improve mortality but make readmission rates go up. Some interventions might actually find people who NEED to be readmitted or they will die.
It is also true that if one dies before 30-days after the index admission, one is less likely to be seen to be readmitted within 30 days. That’s a bias in some of the research that seems to be rarely acknowledged.
Finally, the real fix here is to examine potentially preventable readmissions. I haven’t read deeply yet about those, but the concept and measurement of them exists. A dead person can’t have a potentially preventable readmission, so he’d be excluded from both the numerator and denominator. That makes sense to me. Almost nobody is using PPRs as the dependent variable though, so I still claim a lot of work is biased in a way we don’t want.
For all that, as much as I’ve read, I’ve still only scratched the surface of the readmissions literature. Maybe I’m off base on some of my thinking. That’s where you come in. If you’ve got some expertise in this area, keep me honest, please!